梯度下降优化算法

私以为梯度下降和链式法则是机器学习训练算法的核心。细窥梯度下降的原理对以后处理复杂模型的训练问题会有很大帮助,这里对其进行解释说明。
导数是对一元函数的描述,可以通过观察导数来寻找原函数的特性,导数值是一个标量。
\[f'(x) =\frac{\mathrm{d}f}{\mathrm{d}x}\]对于多元函数,我们使用梯度进行描述。梯度是一个向量,向量的每一个分量是对各参数求偏导的结果。
\[\nabla{f(x_1, x_2}, \ldots , x_n) = \begin{bmatrix} \frac{\partial{f}}{\partial{x_1}}, \frac{\partial{f}}{\partial{x_2}}, \ldots , \frac{\partial{f}}{\partial{x_n}} \end{bmatrix}\]在机器学习中,我们接触的几乎都是多参数问题,为了便于说明和可视化,下面以只有一个参数的函数作为示例。
给出函数:
\[f(x) = \frac{1}{2} x^2\]其导函数为:
\[f'(x) = x\]首先绘制出元函数图像,然后对导数选取少量点进行绘制。虽然导数值是标量,这里根据其大小和符号稍加优化,导数值为正时向右,导数值为负时向左,长度是导数值的大小。
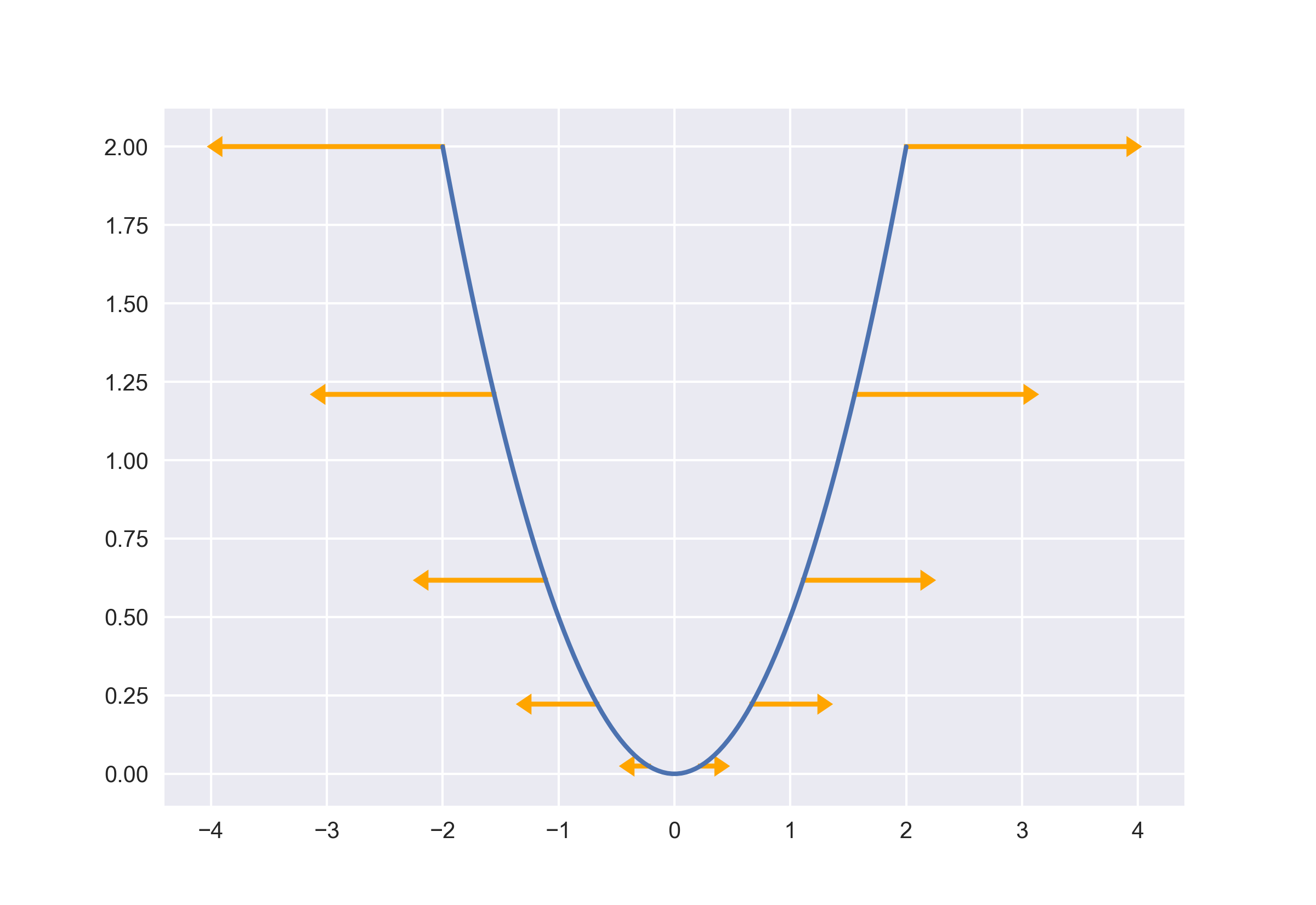
可以发现越陡峭的地方导数值越大。而且对于同坐标系下,导数值的大小也是相当可观的。
我们的目标是寻找 \(x\) 取何值时 \(f(x)\) 的值最小,即:
\[\arg \min_{x} f(x)\]目的是寻找最小值。当 \(f'(x) > 0\) 时,原函数上升,需要把 \(x\) 向左移动;当 \(f'(x) < 0\) 时,原函数下降,需要把 \(x\) 向右移动。
因此,当 \(f'(x) > 0\) 时,\(x \leftarrow x - f'(x)\) 会把 \(x\) 向左移动。
当 \(f'(x) < 0\) 时, \(-f'(x) > 0\),则 \(x \leftarrow x - f'(x)\) 会使 \(x\) 向右移动。
综上两种情况,都是需要使用相同的 \(x \leftarrow x - f'(x)\) 算式对 \(x\) 进行更新,即向导数的反方向移动。
而且注意,这里使用导数的大小作为移动的距离。
因为导数是变化率,有可能会很大,导致每一次移动的距离超过合理范围,所以引入一个步长因子 \(\epsilon\),则每一次的更新操作变为:
\[x \leftarrow x - f'(x) * \epsilon\]取 \(\epsilon = 0.5\)。
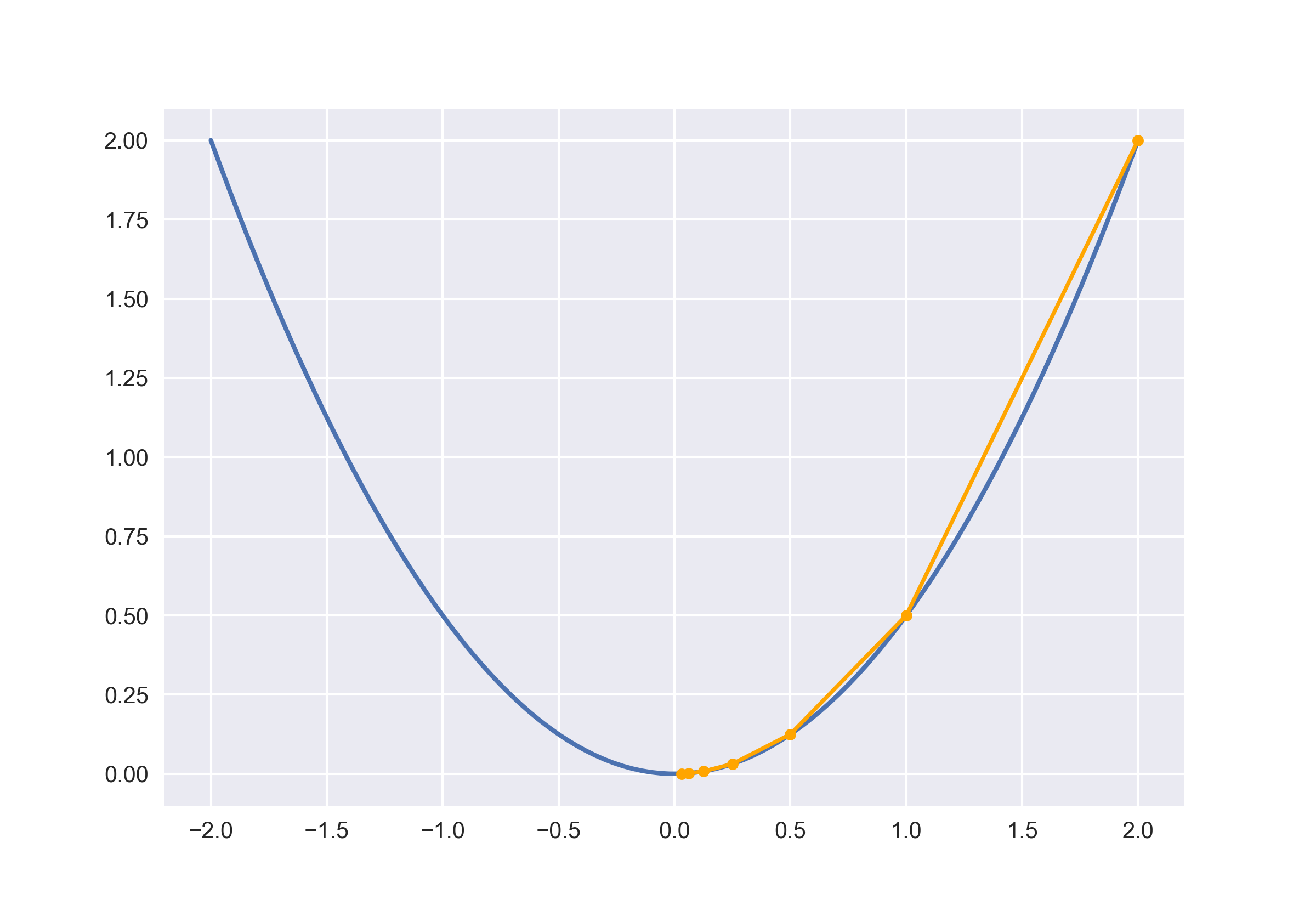
随机初始化 \(x\) 在任意位置,取 \(x = 2\)。此时导数值 \(f'(x) = 2\)。
在 \(x = 2\) 处,计算更新后 \(x\) 的值:
\[x \leftarrow 2 - f'(2) * 0.5 = 2 - 2 * 0.5 = 1\]将 \(x\) 移动到 \(x = 1\) 处。
在 \(x = 1\) 处继续执行更新操作:
\[x \leftarrow 1 - f'(1) * 0.5 = 1 - 1 * 0.5 = 0.5\]在 \(x = 0.5\) 处继续执行更新操作:
\[x \leftarrow 0.5 - f'(0.5) * 0.5 = 0.5 - 0.5 * 0.5 = 0.25\]多次重复后,\(x\) 的值会无限接近最小值点。这里也抛出了梯度下降的一个问题:只会逼近最优解,并不能达到。但是在工程中是完全可以接受的。
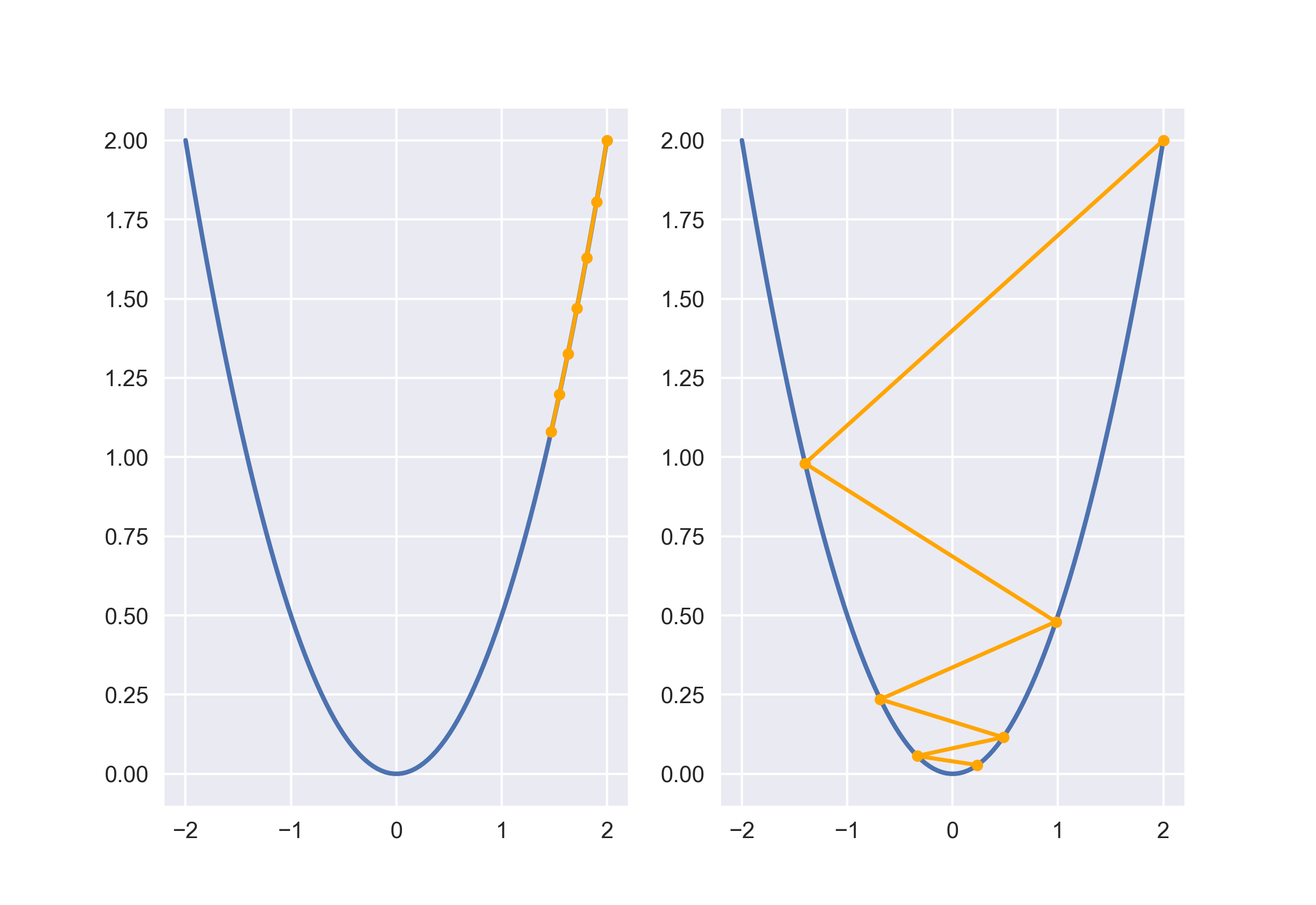
考虑两个极端情况:步长过大、步长过小。通过调整步长因子,迭代相同次数后,可以得到下图的结果。步长太小会极其缓慢接近最小值,而且容易落入局部最小值点。步长过大会发生震荡,导致不稳定。
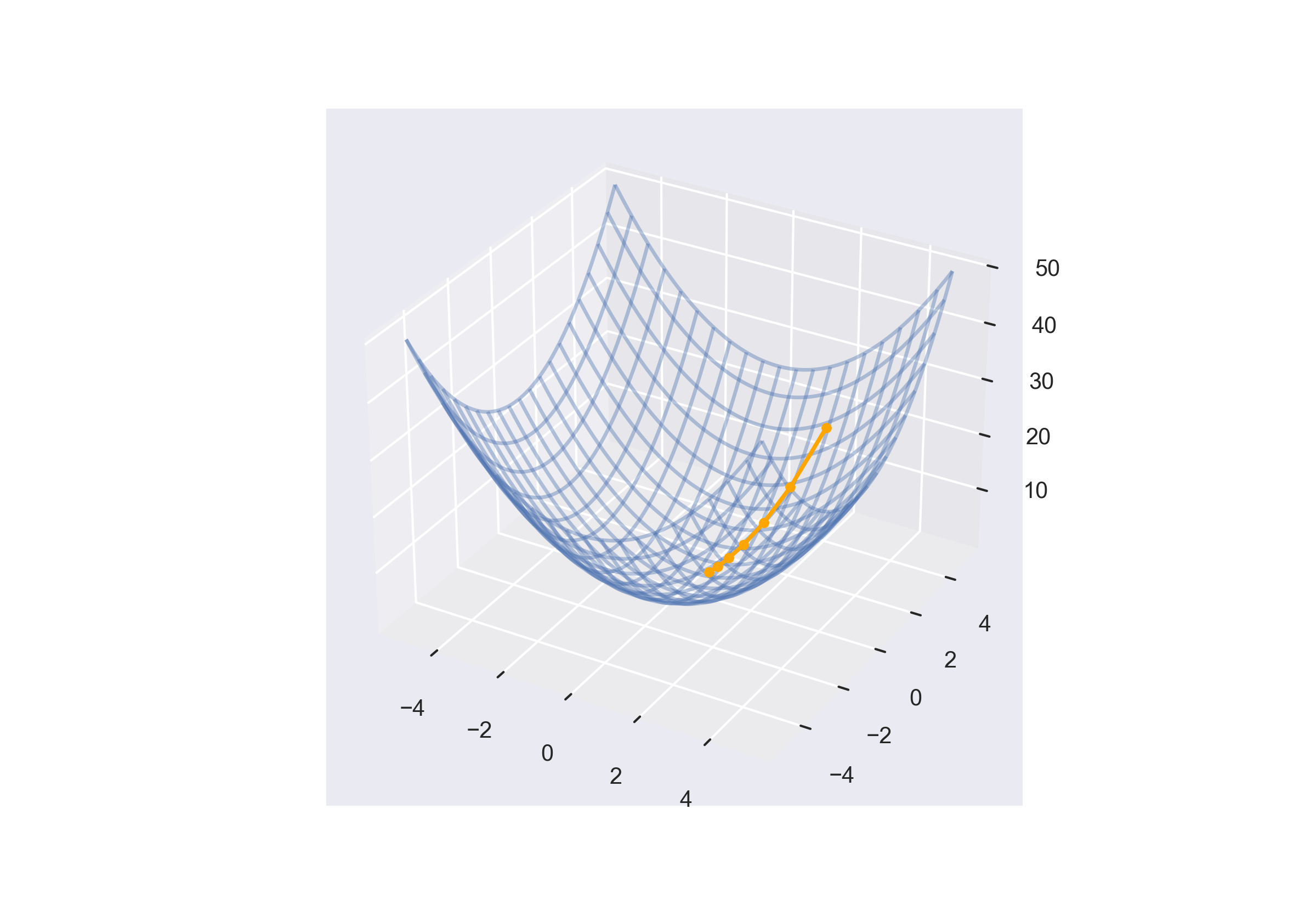
接下来扩展到高维。
梯度是一个向量,表示函数在某一点处最大的增长方向,其大小是在这个方向上的增长率。对于每一个分量,则是该点对于某一维度上的最大斜率。
因为梯度是最大增长方向,为了寻求最小值,需要反向移动。这和一元函数中向导数的所谓反方向移动时相同的。就好比三维世界中,在山坡上放置一个球,球总会沿着下降速度最快的路线滚落到山底。
给出函数:
\[f(x_1, x_2, \ldots , x_n)\]点 \((a, b, \ldots , n)\) 处的梯度为:
\[\nabla{f(a, b, \ldots , n)} = \begin{bmatrix} \frac{\partial{f}}{\partial{x_1}}(a), \frac{\partial{f}}{\partial{x_2}}(b), \ldots , \frac{\partial{f}}{\partial{x_n}}(n) \end{bmatrix}\]引入步长因子 \(\epsilon\) 后的更新操作为:
\[\begin{bmatrix} x_1, x_2, \ldots , x_n \end{bmatrix} \leftarrow \begin{bmatrix} a, b, \ldots , n \end{bmatrix} - \begin{bmatrix} \frac{\partial f}{\partial x_1}(a), \frac{\partial{f}}{\partial{x_2}}(b), \ldots , \frac{\partial{f}}{\partial{x_n}}(n) \end{bmatrix} * \epsilon\]以 \(f(x_1, x_2) = x_1^2 + x_2^2\) 为例,其梯度为:
\[\nabla{f(x_1, x_2)} = \begin{bmatrix} \frac{1}{2}x_1, \frac{1}{2}x_2 \end{bmatrix}\]初始化 \((x_1, x_2) = (2, 4)\),此处的梯度为 \(\begin{bmatrix} 1, 2 \end{bmatrix}\)。
同样使用 \(\epsilon = 0.5\)。
则更新后的 \((x_1, x_2)\) 为:
\[\begin{bmatrix} x_1, x_2 \end{bmatrix} = \begin{bmatrix} 2, 4 \end{bmatrix} - \begin{bmatrix} 1, 2 \end{bmatrix} * 0.5 = \begin{bmatrix} 1.5, 3 \end{bmatrix}\]多次迭代后,绘制出更新路线如下: