LSTM (Long Short Term Memory)

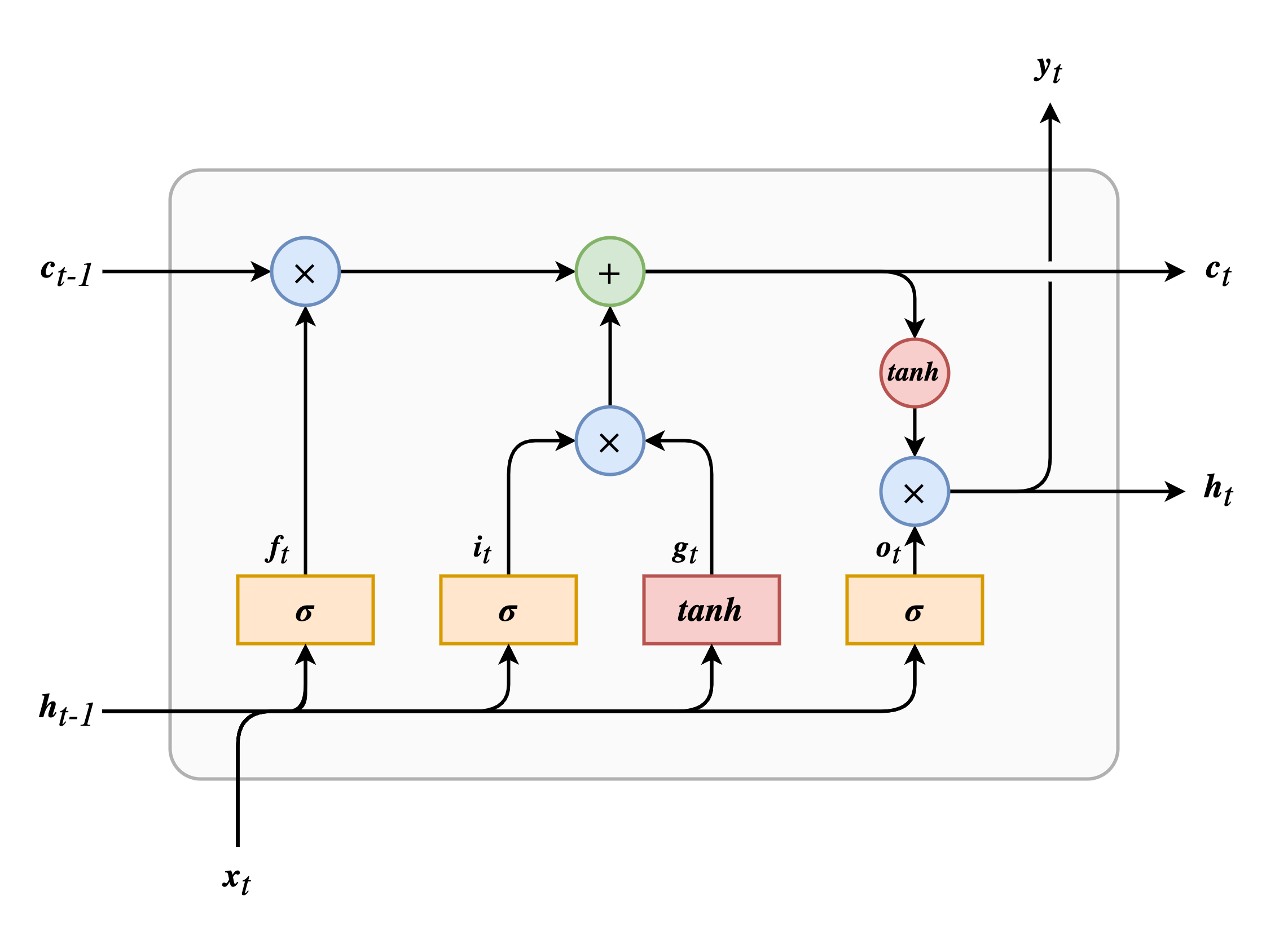
LSTMArchitecture

从 LSTM 结构图上可以看到，除输入 \(\boldsymbol{x}\) 和输出 \(\boldsymbol{y}\) 之外，还有一条短期记忆 \(\boldsymbol{h}\) 和长期记忆 \(\boldsymbol{c}\)。

LSTM 的关键点是长期状态（cell state）。通过训练，网络可以学习如何存储、丢弃和读取长期记忆。在时序遍历时，可以发现 \(\boldsymbol{c}\) 首先通过遗忘门（forget gate）丢弃一些东西；然后使用加法操作添加一些从输入门（input gate）传来的东西；最后通过输出门（output gate）来决定哪些内容作为下一时刻的输入和当前时刻的输出。

下面来细剖一下 LSTM 时如何工作的：

  1. 首先，前一时刻的隐藏状态 \(\boldsymbol{h}_{t-1}\) 和当前时刻的输入 \(\boldsymbol{x}_t\) 一起传入四个全连接层，其中三个使用 \(sigmoid\) 作为激活函数生成三个不同的门控向量（遗忘门 \(\boldsymbol{f}_t\)，输入门 \(\boldsymbol{i}_t\)，输出门 \(\boldsymbol{o}_t\)），剩余一个使用 \(\tanh\) 作为激活函数生成输入门的输入数据（\(\boldsymbol{g}_t\)）；
  2. 长期记忆 \(\boldsymbol{c}_{t-1}\) 首先通过遗忘门，由遗忘门的门控向量控制哪些记忆应当被删除；
  3. 输入门又称更新门，控制需要将哪些信息添加到长期记忆中。这里的信息数据由 \(\boldsymbol{h}_{t-1}\) 和 \(\boldsymbol{x}_t\) 共同生成。通过输入门的数据使用加法操作被添加到长期记忆中；
  4. 之后长期记忆生成两个分支，其中一支作为下一时刻的 \(\boldsymbol{c}_{t-1}\) 直接输出。另外一支首先经过 \(\tanh\) 激活函数，然后通过输出门决定哪些数据可以作为下一时刻的短期记忆 \(\boldsymbol{h}_{t-1}\) 和当前时刻的输出 \(\boldsymbol{y}_t\)。

三个门控单元由输入 \(\boldsymbol{x}\) 和短期状态 \(\boldsymbol{h}\) 生成：

\[\boldsymbol{f}_t = \sigma (\boldsymbol{W}_{xf} \boldsymbol{x}_t + \boldsymbol{W}_{hf} \boldsymbol{h}_{t-1} + \boldsymbol{b}_f)\] \[\boldsymbol{i}_t = \sigma (\boldsymbol{W}_{xi} \boldsymbol{x}_t + \boldsymbol{W}_{hi} \boldsymbol{h}_{t-1} + \boldsymbol{b}_i)\] \[\boldsymbol{o}_t = \sigma (\boldsymbol{W}_{xo} \boldsymbol{x}_t + \boldsymbol{W}_{ho} \boldsymbol{h}_{t-1} + \boldsymbol{b}_o)\]

这里使用 \(sigmoid(\sigma)\) 作为激活函数，该函数的特点是其值域为 \((0, 1)\)，当取值接近 \(0\) 时表示需要阻断，接近 \(1\) 时表示放行。

输入门的的输入数据 \(\boldsymbol{g}_t\) 的激活函数为 \(\tanh\)，\(\tanh\) 将值域扩展为 \((-1, 1)\)，这样增加了取值范围，同时也起到了正规化的作用：

\[\boldsymbol{g}_t = \tanh (\boldsymbol{W}_{xg} \boldsymbol{x}_t + \boldsymbol{W}_{hg} \boldsymbol{h}_{t-1} + \boldsymbol{b}_g)\]

上述四个公式中：

\(\boldsymbol{W}_{xf}\)、\(\boldsymbol{W}_{xi}\)、\(\boldsymbol{W}_{xo}\)、\(\boldsymbol{W}_{xg}\) 是输入 \(x\) 的权重矩阵；

\(\boldsymbol{W}_{hf}\)、\(\boldsymbol{W}_{hi}\)、\(\boldsymbol{W}_{ho}\)、\(\boldsymbol{W}_{hg}\) 是短期状态 \(h\) 的权重矩阵；

\(\boldsymbol{b}_f\)、\(\boldsymbol{b}_i\)、\(\boldsymbol{b}_o\)、\(\boldsymbol{b}_g\) 是偏置向量。

LSTM 的计算过程：

\[\boldsymbol{c}_t = \boldsymbol{f}_t \otimes \boldsymbol{c}_{t-1} + \boldsymbol{i}_t \otimes \boldsymbol{g}_t\] \[\boldsymbol{y}_t = \boldsymbol{h}_t = \boldsymbol{o}_t \otimes \tanh (\boldsymbol{c}_t)\]

GRU (Gated Recurrent Unit)

LSTM 在 1997 年首次被提出，其后出现了多种变体进行改进。2014 年出现的 GRU 以其更少的参数数量，且与 LSTM 相比并未出现明显下滑的性能，得到人们的青睐。

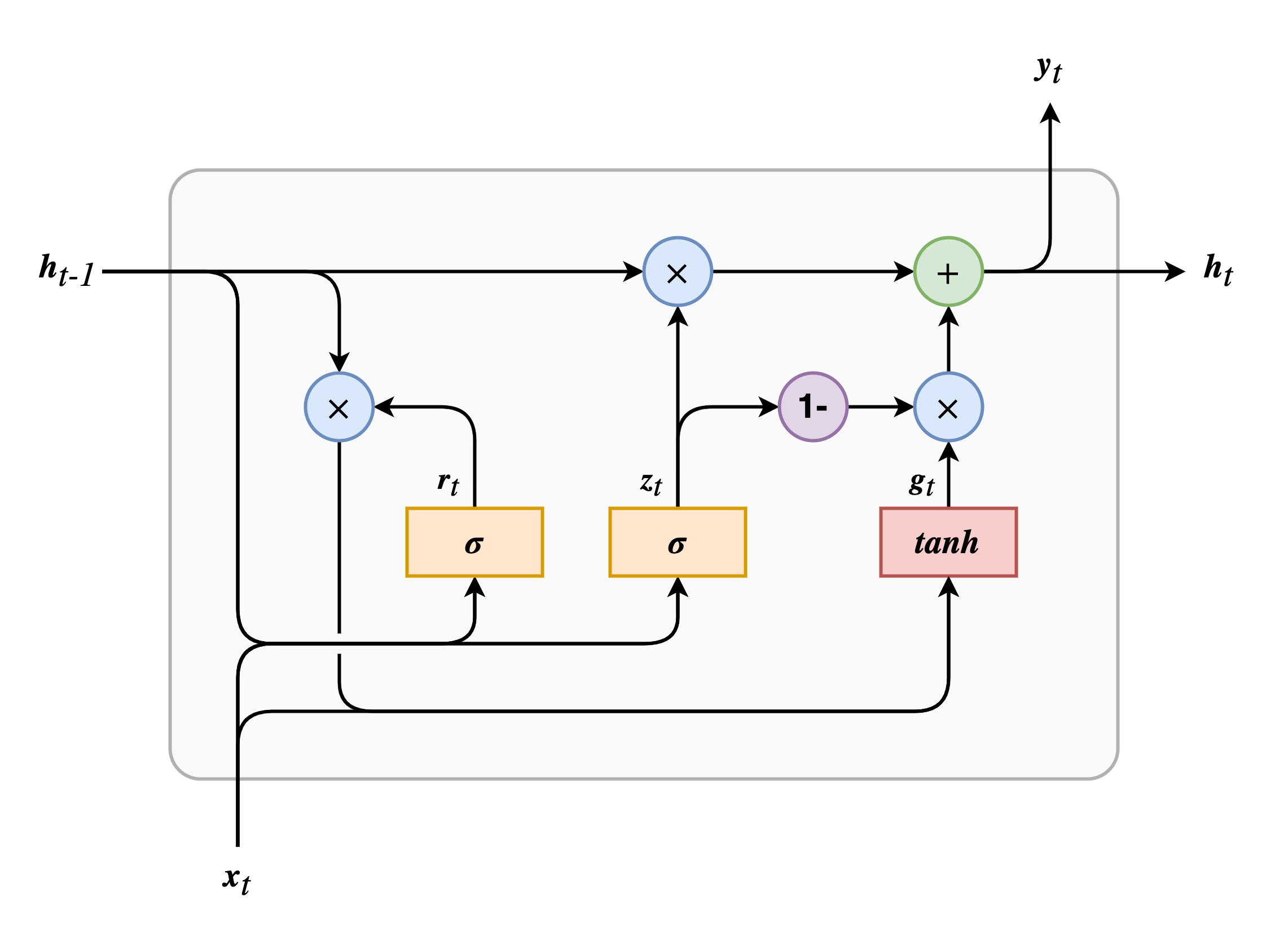
GRUArchitecture

GRU 相比于 LSTM 做出的改变有：

  1. 长期记忆和短期记忆被合并成一个 \(\boldsymbol{h}_t\)；
  2. 遗忘门和输入门被合并成一个 \(\boldsymbol{z}_t\)，称为更新门（update gate），如果门控变量为 \(1\) 则遗忘门打开，因为 \(1 - 1 = 0\) 则输入门关闭。即想要记住某些信息前，需要先腾出空间，删除对应位置的信息；
  3. 增加一个称为重置门（reset gate）的门控单元 \(\boldsymbol{r}_t\)，用来控制前一时刻状态的哪些部分可以被添加到记忆中。
  4. 没有输出门，每一时刻完整的状态向量同等的作为输出向量。

GRU 的计算过程：

\[\boldsymbol{z}_t = \sigma (\boldsymbol{W}_{xz} \boldsymbol{x}_t + \boldsymbol{W}_{hz} \boldsymbol{h}_{t-1} + \boldsymbol{b}_z)\] \[\boldsymbol{r}_t = \sigma (\boldsymbol{W}_{xr} \boldsymbol{x}_t + \boldsymbol{W}_{hr} \boldsymbol{h}_{t-1} + \boldsymbol{b}_r)\] \[\boldsymbol{g}_t = \tanh (\boldsymbol{W}_{xg} \boldsymbol{x}_t + \boldsymbol{W}_{hg}(\boldsymbol{r}_t \otimes \boldsymbol{h}_{t-1}) + \boldsymbol{b}_g)\] \[\boldsymbol{y}_t = \boldsymbol{h}_t = \boldsymbol{z}_t \otimes \boldsymbol{h}_{t-1} + (1 - \boldsymbol{z}_t) \otimes \boldsymbol{g}_t\]

Vanilla RNN

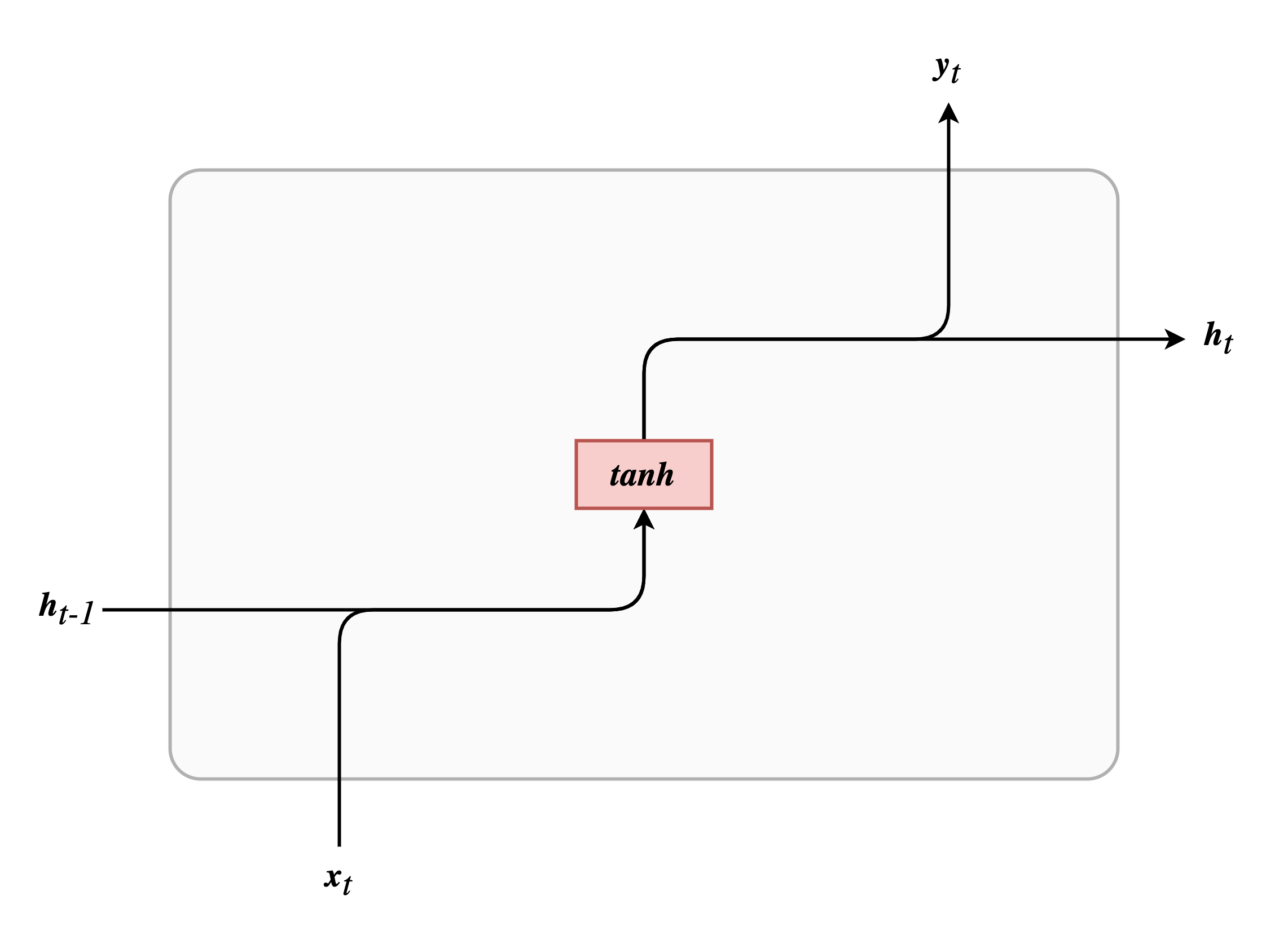
最后给出最基本的 RNN 的结构图，对比发现是多么的朴实无华：

VanillaRNNArchitecture